I’ve seen many people stumbling over collision detection for games. It’s a bit complicated to explain, so I figured I’d make one article I could link to.

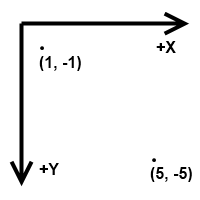
First, understand your coordinate space. (0, 0) is the top-left of the monitor. To the right, X increases. Going down, Y increases. (0, 1) is down from (0, 0). (1, 0) is right of (0, 0). It’s important to remember this because you’re going to have to do 2D geometry in this coordinate space.

What does it mean for two objects to collide? The simplest form of collision detection treats all objects as rectangles and decides that two objects collide if their rectangles touch or overlap.

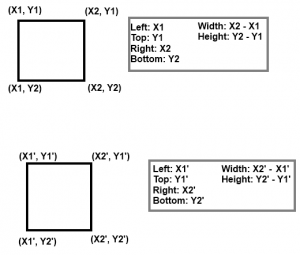
To determine if two rectangles collide, you have to have a way to represent them. There’s many ways to look at a rectangle, and .NET gives you properties to support all of them:

• A point that represents the top-left corner, a width, and a height.
• A point that represents the top-left corner and a point that represents the bottom-right corner.
• Four integers that represent the x coordinate of the left side, the y coordinate of the top side, the x coordinate of the right side, and the y coordinate of the bottom side. (This is known as LTRB for “left, top, right, bottom.)

When doing collision math, I tend to work with the LTRB form. When drawing rectangles, I prefer the two-point form. For the purposes of discussion, look at the image to see the names I’ll use for each rectangle in collision detection. Rather than try to fiddle with X1, X2, X3, X4, I’ll refer to the coordinates of the 2nd rectangle as X1′ (read “ecks one prime”) to indicate it’s coordinates of a different rectangle. I also annotated how LTRB maps to this, and included how you’d get width and height. I will be assuming that X1 > X2, Y1 > Y2, and so forth; if you don’t hold those rules this math gets much more tricky. I will order all of my examples to use < for the comparison because things would be more confusing otherwise. My examples require overlap for a collision; if you want to have touching objects collide replace my < with <=.

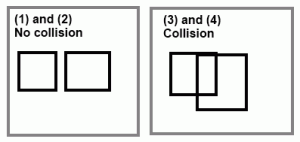
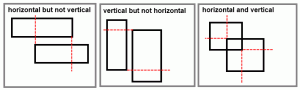
Now we have to talk about all the possible ways rectangles could collide with each other. Let’s talk horizontal scenarios first. The imageshows the four scenarios; I combined them into two images since the difference is which rectangle you consider “first”. I will refer to the rectangle with X1, X2, and so forth as “r1” and the one with X1′, X2′, etc. as “r2”. Here’s the four scenarios:

1. In this case, we check if r2’s left edge is between r1’s left and right edges. That is, if X1 < X1′ < X2 we have a collision. X1 < X1′, but X1′> X2 so there is no collision.
2. In this case, we check if r2’s right edge is between r1’s left and right edges. That is, if X1 < X2′ < X2 we have a collision.
3. (1), but there is a collision because X1 < X1′ < X2.
4. (2), but there is a collision because X1 < X2′ < X2.

That’s fairly easy to translate into code:

Dim isHorizontalCollision As Boolean = False

' Check left edge of r2
If r1.Left < r2.Left AndAlso r2.Left < r1.Right Then
   isHorizontalCollision = True
End If

' Check right edge of r2
If r1.Left < r2.Right AndAlso r2.Right < r1.Right Then
isHorizontalCollision = True
End If

This is only half the story for reasons that will be illustrated later. For there to be a collision there has to be a vertical collision as well.

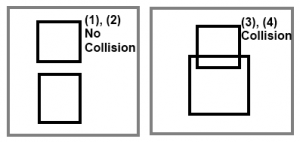
The image illustrates, here’s the cases (shortened since they are analogous):

1. Check r2’s top edge; collision if Y1 > Y1′ > Y2. No collision in this case because Y1′ > Y2.
2. Check r2’s bottom edge; collision if Y1 > Y2′ > Y2. No collision in this case because Y2′ < Y1.
3. Similar to (1), but this time Y1 > Y1′ > Y2 so there is a collision.
4. Like (2) but Y1 > Y2′ > Y2 so there is a collision.

There’s a trick here; since moving down the monitor increases the value of the Y coordinate, we have to invert our assumptions of up and down. Normally, Y < Y’ would indicate Y’ is above Y, but on the monitor it indicates Y’ is below Y. The code addresses this by rearranging the comparisons.

Dim isVerticalCollision As Boolean = False

' Check top edge of r2
If r1.Top < r2.Top AndAlso r2.Top < r1.Bottom Then
    isVerticalCollision = True
End If

' Check bottom edge of r2
If r1.Top < r2.Bottom AndAlso r2.Bottom < r1.Bottom Then
    isVerticalCollision = False
End If

There’s one case these rules don’t catch. What if r1 is completely inside of r2? Neither edge of r2 will be in r1, so all of the tests will fail.

I have a feeling this is why I’ve never seen anyone use this method of collision detection before. However, since it’s the only overlapping case I can think of where no edges of r2 are between the edges of r1, we can special-case it in each check. This scenario happens whenever X1′ < X1 and X2′ > X1. The test could be more complicated, but if we know no edges of r2 are between the edges of r1 then there *must* be a collision if the left edge of r1 is between the top and bottom edges of r2. (Likewise, we can test the top of r1 is between top and bottom of r2.) If you don’t trust me, try to draw a case where it is true that no edges of r2 are inside r1, the left edge of r1 is between r2’s edges, and the right edge of r1 is outside of r2’s edges. You’ll find it impossible. I’d add this to the collision detection:

Dim isContainsCollision As Boolean = True

If Not isHorizontalCollision AndAlso Not isVerticalCollision Then
    If r2.Left < r1.Left AndAlso r1.Left < r2.Right Then
        If r2.Top < r1.Top AndAlso r1.Top < r2.Bottom Then
            isContainsCollision = True
        End If
    End If
End If

Except in that special case, a collision only exists if there is both a vertical and horizontal collision. Why?

The image illustrates. The dashed red lines are where edges overlap according to one of the tests.

After you do all of those tests, there is a collision if either the horizontal and vertical checks indicate a collision *or* r1 contains r2. That is, the final collision check if you’re interested in a yes or no answer would look like this:

If (isHorizontalCollision AndAlso IsVerticalCollision) OrElse isContainsCollision Then
    ' There is a collision.
End If

Now here’s the fun part: I only went over this because I wanted you to understand the math behind everything. If you use the System.Drawing.Rectangle structure, the IntersectsWith() method will tell you if one rectangle collides with another. Many .NET programmers don’t use controls for games but instead keep track of Rectangle objects for each entity that they use when drawing in the Paint event. This makes collision detection easy. Novice programmers tend to use many PictureBox controls, but that doesn’t mean you have to do things the hard way! Every control has a Bounds property; this returns a Rectangle that indicates the control’s bounds. To detect if two picture boxes collide, you might write code like this:

Function IsCollision(ByVal r1 As PictureBox, ByVal r2 As PictureBox) As Boolean

    Return r1.IntersectsWith(r2)

End Function

This isn’t the only way to do collision detection in games, but it is the easiest. The links below point to projects that demonstrate.

• VS 2010
• VS 2008